Černé díry a superradiace

Černá díra (FromQuarkstoQuasars.com)

V obecném pojetí je superradiace efekt, který vzniká při rozptylu vlny na správně rotujícím objektu. V tomto článku kromě něj nakousneme i tzv. Penroseovy jevy, které souvisí s nalétáváním částic na rotující černou díru. Nakonec si řekneme, že superradiace platí i pro elektromagnetické vlny rozptýlené na vodivých objektech.

Superradiaci popisuje článek [1], kterým jsou podloženy výsledky shrnuté v tomto článku.

Zmiňme ještě na začátek, že anglický pojem superradiance vystihuje více fyzikálních jevů. O jednom zde budeme mluvit. Shodou okolností se ale stejně jmenuje i zesilování jasnosti za pomoci koherentních zářičů. Tento typ superradiace zde ale popisovat nebudeme.

Černé díry

Už v prosinci roku 1915 přišel Karl Schwarzschild v plné polní na sféricky symetrické řešení Einsteinových rovnic, které lze zapsat ve tvaru

které nemusíme více rozebírat. Taková metrika popisuje libovolné sféricky symetrické pole. Sám Schwazschild poté vyzkoušel případ, při němž teorie relativity popisuje hmotný bod. Zjistil, že takové řešení není těžké, dnes nazýváme takový objekt Schwarzschildova černá díra. Po Schwarzschildovi přišli pánové Reissner a Nordström, kteří se rozhodli bodové hmotnosti přiřadit ještě náboj. Jejich řešení dnes nazýváme Reissner-Nordströmovo řešení a objektu, který popisuje, říkáme elektricky nabitá černá díra.

Černá díra, hmota zahuštěná pod Schwarzschildův poloměr (Dscovery.com)

Co to ale černá díra přesně je?

Ve stručnosti se dá v řešení rovnic zjistit, že existuje tzv. Schwarzschildův poloměr , tedy dvojnásobek hmotnosti objektu. Jedná se o sféru okolo objektu, na které je úniková rychlost rovna rychlosti světla. Výše byl zmíněný hmotný bod, ale zároveň bylo řečeno, že daná metrika popisuje libovolné sféricky symetrické těleso, černá díra je poté libovolná koule, jejíž poloměr je menší než Schwarzschildův. Jak je to se skutečnou velikostí, není jednoduché zjistit. Lze předpokládat jakousi setrvačnost platnosti fyzikálních rovnic, abychom při kolapsu řekli, že každá černá díra se zhroutí do bodu, čímž vytvoří singularitu, kde je pravda, však v důsledku nulového experimentálního poznání z místa za horizontem bohužel nevíme. Vnější vlastnosti černé díry jsou totiž stejné, ať se jedná o kouli o poloměru téměř Schwarzschildovu, nebo o hmotný bod.

Po rozboru sféricky symetrických černých děr už není problém představit si ty axiálně symetrická. Axiální symetrie představuje symetrii podle nějaké osy. Např. válec je totálně axiálně symetrický podél své hlavní osy. Takové prostoročasy už není jednoduché popsat a metrika, která jim přísluší, je až příšerně složitá, proto ji zde nebudeme uvádět, ale lze se na ni podívat např. na [2].

Obecně však platí, že každou černou díru lze popsat čtyřmi konstantami:

• M – hmotnost černé díry,
• Q – elektrický náboj černé díry,
• J – moment hybnosti (otáčení) černé díry,
• S – „magnetický náboj“ černé díry.

Klasifikace černých děr

Jelikož neznáme v reálném Vesmíru magnetické monopóly, je S = 0. Uvádí se často kvůli tomu, že má svůj speciální význam z algebraického hlediska při rozboru. Podle náboje a momentu hybnosti pak černé díry dělíme na:

• : Schwarzschild,
• : Reissner-Nordström,
• : Kerr,
• : Kerr-Newman.

Zbývá nám probrat Kerrovu a Kerr-Newmanovu černou díru. Díky složitosti metriky není jednoduché intuitivně ukázat, proč se tak děje, nicméně existují zde dva specifické horizonty (různých horizontů je ve skutečnosti daleko více, přestože je známý jen horizont události díky sci-fi kultuře). Tyto horizonty vymezují důležitou oblast, které se říká ergosféra. Právě o ní pojednáme v další podkapitole.

Superradiace a Penroseovy jevy v ergosféře

Kerrova černá díra se pyšní s ve Vesmíru ojedinělým prostředím, jemuž říkáme ergosféra. Více o ergosféře lze najít na wikipedii [3]. Právě rotující černá díra má zajímavou vlastnost, a to tu, že nerotuje sama. Společně s ní rotuje i samotný prostoročas. Tomuto efektu říkáme dragging a jedná se skutečně o strhávání prostoru rotujícím objektem. V určité vzdálenosti od černé díry potom dojde k tomu, že prostoročas rotuje rychlostí světla. Oblast pod touto tzv. statickou mezí až ke Schwarzschildově horizontu (R = 2M) nazýváme ergosférou.

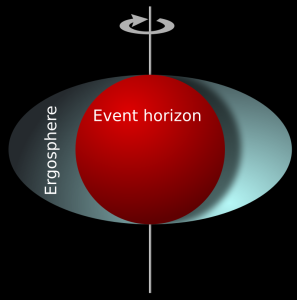
Ergosféra oddělená statickou mezí a horizontem (Wikipedia.org)

Ergosféra má několik zajímavých vlastností. V tomto článku se zaměříme na efekty doprovázející rozptyl na rotující černé díře.

Pokud letí částice směrem k černé díře, která má nenulový moment hybnosti, musí dříve nebo později dosáhnout statické meze, v němž prostoročas rotuje rychlostí světla. Jakmile proletí touto hranicí, dostane se do ergosféry, kde se rozpadne na dvě různé částice. Stále musí platit, že se zachovává energie. Jedna z částic pokračuje dál s vyšší energií, než měla částice původní, druhá musí mít tedy zápornou hmotnost. Skutečně tato částice poté spadne do černé díry, čímž sníží její celkovou hmotnost a energii.

Superradiace je jev stejného charakteru, jen na rotující černou díru dopadá vlna, která se rozpadne na dvě různé složky. Na rozdíl od částic popisujeme v klasické (rozumějme nekvantové) fyzice vlny pomocí polní teorie. Energie takového pole se potom musí zachovat, a proto opět vlna, kterou ergosféra propustí do černé díry, musí mít zápornou energii.

Tímto způsobem se dříve fyzici snažili vysvětlit vysokou zářivost objektů s výrazným rudým posuvem. Ty jsou od nás totiž podle modelu expandujícího Vesmíru velice daleko, a tudíž je zvláštní, že je vidíme. Musí být extrémně jasné, svítivé. Jednou z myšlenek bylo, že se jedná o záření odražené od několika rotujících černých děr v jádrech galaxií. I takový efekt by ale byl velice slabý, jak se později spočítalo. Přidalo se proto do teorie černou díru obíhající plazma, o tom ale jindy.

Superradiace v teorii EM pole

Po vzoru předchozího jevu, který je možný v důsledku strhávání prostoročasu, napadlo fyziky podívat se na kloub vysoce podobnému jevu. Oblasti fyziky, která studuje strhávání prostoročasu, se totiž neříká gravitomagnetismus pro nic za nic. Jedná se skutečně o Einsteinem nalezený jev, který bychom mohli nepřesně označit jako indukci gravitace. Pokud tedy superradiace funguje na úrovni gravitomagnetismu, proč by nemohla fungovat i na úrovni elektromagnetických teorií?

Jakov Zeldovič tak přišel s modelem rotujícího vodivého válce, na nějž pustil elektromagnetickou válcovou vlnu. Jak očekával, pokud splnil podmínku , které se dnes říká Zeldovičova-Misnerova podmínka superradiace, byl výkon odchozí vlny vyšší než výkon vlny dopadlé za působení síly na válec proti směru otáčení. Pokud tak udržujeme konstantní úhlovou frekvenci válce , musí zabrat motor, který válec roztáčí, z něj se bere ona energie, kterou si strhává vlna.

Pro vysvětlení dodejme, že je úhlová frekvence dopadající vlny (barva) a je počet period v azimutálním směru.

Zdroje
[1] ArXiV – The many faces of superradiance
[2] Wikipedie – Kerr-Newman metric; https://en.wikipedia.org/wiki/Kerr%E2%80%93Newman_metric
[3] Wikipedie – Ergosféra; https://cs.wikipedia.org/wiki/Ergosf%C3%A9ra