Co je to kvantová mechanika?

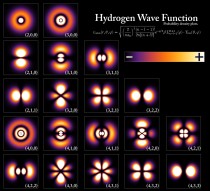
Vlnová funkce vodíku (Wikipedia.org)

Fyzika prodělala na počátku 20. století změny, které pociťujeme dodnes. Teorie relativity a kvantová mechanika navždy změnily způsob chápání našeho světa a Vesmíru, v němž žijeme. Kvantová teorie dodnes straší mnohé studenty. Podívejme se, proč je tato teorie pro mnohé lidi tak neuchopitelná.

Před kvantovou mechanikou

Když Isaac Newton formuloval své pohybové zákony, měl už jistě v mysli velký matematický aparát, pomocí nějž se tyto zákony staly kvantitativním produktem. Pokud se použije např. síla působící na daný objekt, říká Newton, že odpovídající funkce popisující polohu tělesa v čase, splní rovnici

kde je zrychlení ve směru . Matematicky se jedná o druhou derivaci polohy, tj. změnu změny polohy. Zmíněná rovnice se nazývá diferenciální a právě diferenciální rovnice jsou to, co definuje počítání v Newtonovské mechanice. Řešením výše zmíněné rovnice je funkce

kterou známe ze základních škol. Jednoduše se zde také nahlédne známý vztah , který si normálně musíme pamatovat.

Obecně ke kvantové mechanice

Klasická mechanika se řídí pohybovými rovnicemi a elementární objekt, který je třeba najít, je zobrazení udávající polohu v čase. Dá se říci, že každá fyzikální teorie potřebuje svůj elementární objekt, který se snaží najít. Pro takový objekt musí teorie formulovat evoluční rovnice (rovnice vývoje objektu v čase), okrajové podmínky (hodnotu v nějakém speciálním bodě) a počáteční podmínky (hodnotu objektu při spuštění systému).

V praxi to funguje tak, že fyzik vyřeší rovnice a dostane nějaké obecné řešení. Na něj poté naklade spousty podmínek, aby získal přesnější výraz. V našem případě s harmonickými kmity z předešlé části by se jednalo o nalezení konstant .

Jak může vypadat kvantový svět (GizMag.com)

Kvantová mechanika je ale těžší teorie než klasická mechanika. Je třeba úplně opustit jakoukoliv představu přesné trajektorie částic a vyjít z něčeho fundamentálnějšího pro fyziku, než jsou krásné konstrukce teorií, a z experimentálních výsledků. Právě ty totiž vedly ke zrodu kvantové mechaniky. Pokud je ale měření hlavní částí teorie, neznamená to, že se bude jednat o statistickou teorii?

Znamená! Kvantová mechanika je skutečně teorie založená na pravděpodobnosti. Dnes všude uznávaná Kodaňská interpretace QM říká, že elementární objekt kvantové mechaniky je vlnová funkce (tu si představme jako vektor – šipku, kterou známe už ze střední školy). Velikost tohoto vektoru potom svým způsobem udává pravděpodobnost naměření částice v nějakém předem udaném objektu.

Napadá vás, že touto cestou lze popisovat nejen částice, ale také vlny? Potom máte zajisté pravdu. Dokonce formalismus kvantové mechaniky vůbec nerozlišuje mezi částicí a vlnou, což byl jeden z problémů, který neuměla klasická fyzika pojmout – proč se neutron chová jako vlna i jako částice a stejně tak i světlo?

Kvantová mechanika na otázku ohledně korpuskulárně-vlnového dualismu neodpověděla, ba co víc se dokázala této otázce úplně vyhnout a dává správné, experimentálně ověřené výsledky!

Kvantová mechanika coby teorie

Skalární součin (MathInsight.org)

Pojďme se nyní společně podívat na to, jak ta úžasná teorie vlastně vypadá. Ústředním pojmem je tedy jakási šipka, kterou si můžeme představit jako n-tici čísel . Pokud budeme mít takové šipky dvě, můžeme provést jejich skalární součin známým způsobem

Velikost tohoto skalárního součinu udává, jak moc je obsažen v . To si můžeme představit za pomoci obrázku vpravo, na němž vidíme, že skalární součin je velikost projekce jednoho vektoru do druhého.

Pokud vezmeme tuto hodnotu skalárního součinu v kvadrátu, to znamená vezmeme číslo

dostaneme to, co Kodaňská interpretace QM definuje jako pravděpodobnost nalezení stavu ve stavu .

Elementární objekt v QM ale raději značíme jako a skalární součin jako . Proč? To je tajemství fyziků známé pod pojmem Diracova notace.

Máme tedy elementární objekt, jeho okrajové a počáteční podmínky můžeme kdykoliv stanovit. Nezbývá už nic jiného než zjištění dynamických rovnic, které popisují stav v kvantovém světě. Je ve skutečnosti jen jedna a všichni ji známe, je to slavná Schrödingerova rovnice. Erwinu Schrödingerovi byla společně s Paulem A. M. Diracem udělena Nobelova cena za fyziku roku 1933 právě za kvantovou teorii. Rovnice má v nejsnazším pojetí tvar

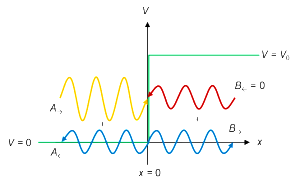
Potenciálová bariéra (Wikipedia.org)

kde je hybnost a význam (tzv. potenciálu) můžeme vidět na obrázku vlevo. Co na obrázku nevidíme, je to, že čím větší potenciál je, tím více se v pravé části obrázku vlna utlumí. Pro nekonečně velký potenciál pak vlna za překážku vůbec nedojde.

Jak taková překážka vypadá v praxi? Může se jednat o stínítko, na které dopadá foton.

V hybnosti se navíc skrývají druhé derivace podle prostoru, takže rovnice se nedá řešit tak snadno, jak by se dalo říci na první pohled, že , tak to nikdy fungovat nemůže.

Atom vodíku

Nejsnazší aplikací kvantové mechaniky je atom vodíku, kde za potenciál dosadíme Coulombův potenciál známý z elektrostatiky. Po dosazení do Schrödingerovy rovnice potom vychází různé stavy – šipky, které nazýváme vlnovými funkcemi. Ještě jsme nezmínili, že tyto vektory, vlnové funkce nebo stavy, lze vyjádřit v libovolných souřadnicích. Může se jednat o polohy, hybnosti nebo se může jednat o energetický popis.

Představme si ale nyní, že vyjádříme vlnovou funkci v závislosti na souřadnicích a označíme ji . Ve skutečnosti bychom tak udělali projekcí . Pro znalé integrálů definujme

a nyní je jasné, že udává pravděpodobnost, že se částice nalézá v objemu . Nezbývá než říct, že částice existuje, a tudíž musí nekonečný objem dát jednotkovou pravděpodobnost, což je okrajová podmínka kvantové teorie pro částici. S touto vlastností se vraťme k úplně prvnímu obrázku celého článku, kde je právě pro atom vodíku ukázané, s jakou pravděpodobností se nachází elektron a v jakém prostoru okolo jádra atomu. Jednotlivé elektrony jsou „očíslovány“ hodnotami (n, l, m).

Pokud potom je elektron v nějakém stavu (n, l, m), můžeme zjistit nějakou jeho vlastnost – hodnotu spinu, například. Jak to uděláme? Definujeme ke spinu příslušné zobrazení a zkoumáme jeho vlastnosti. Jak se tento proces dělá, je však na příliš složité povídání.

Shrnutí

Kvantová mechanika je tedy teorie, která si bere jako objekt zkoumání rozdělení pravděpodobnosti v prostoru prostřednictvím vektory/stavy/vlnové funkce. Ty potom nechává vyvíjet podle Schrödingerovy rovnice. V každém stavu lze změřit hodnoty fyzikálních veličin za pomoci jim příslušících zobrazení.

Na příště si necháme povídání o kvantové provázanosti a neurčitosti.

A proč je tedy tato teorie natolik neuchopitelná? Už v jejím základním principu. Vlnové funkce žijí na velkých vektorových prostorech se skalárním součinem, takovým říkáme Hilbertovy prostory. A na těchto Hilbertových prostorech, které mohou být nekonečně-dimenzionální existují zobrazení odpovídající fyzikálním veličinám. Zobrazují ale vlnové funkce na jiné vlnové funkce. Jenže nic jako vlnová funkce ve skutečném světě neexistuje, tak jak to můžeme zobrazit něčím měřitelným?

Zdroj:
A condensed course of quantum mechanics, Pavel Cejnar, Karolinum 2013